İĞNELİ ELEKTRO LİF ÇEKİM İŞLEMİ

İğneli Elektro Lif Çekimi İşlemi

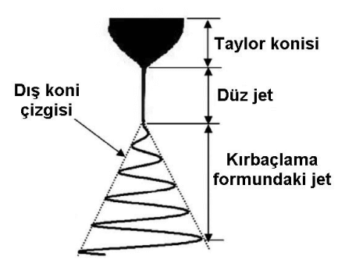
Tek iğneli elektro lif çekim sisteminde, iğnenin ucundaki damlacık, elektrostatik itme ve yüzey gerilimi olmak üzere iki zıt kuvvete maruz kalır. Elektrostatik itme, bir sıvının yüzey geriliminin üstesinden gelmeye başladığında, iğnenin ucundaki asılı damla, Taylor konisi olarak bilinen konik bir damlacık şeklinde deforme olur. Elektrostatik kuvvet yüzey geriliminin üstesinden geldiğinde, solüsyonun yüklü ince bir polimerik jeti iğne ucundan dışarı çıkar. Bu iki kuvvet arasındaki etkileşim, jet akımını uzatır ve çözücünün buharlaşmasına yol açan bir kamçılama hareketine maruz kalmasını sağlar. Bu durum, jet akımının uzun ve ince bir filament olarak sürekli uzamasına neden olur. Bu filament katılaşır ve sonunda topraklanmış bir toplayıcı üzerine biriktirilir ve bu da düzenli bir lif oluşumu ile sonuçlanır. Buna ek olarak, elektro lif çekiminde jet davranışı

Şekil 1.18‘ de gösterilmekte olan üç ana aşamaya ayrılabilir.

• Taylor konisinin oluşumu,
• Düz hale gelen jetin fırlatılması,
• Kararsız kırbaçlama hareketinin olduğu jet bölgesi

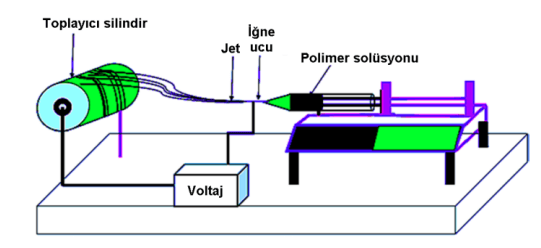
Şekil 1.19‘ da gösterilen tek iğneli elektro lif çekim sisteminde otomatik dozajlama yapabilen bir pompa üzerine yerleştirilmiş şırınga içerisine viskozitesi akışa uygun polimer solüsyonu ile doldurulur. Daha sonra belirlenen solüsyon akış hızına göre dozajlama başlatılır ve şırıngaya bağlı iğne ucunda damla şeklindeki Taylor konisi oluşumu gerçekleşir. Yüksek gerilime sahip güç kaynağı vasıtasıyla bir ucu iğne ucuna diğer ucu topraklanmış toplayıcı silindire bağlı olan alana belirlenen gerilim uygulanır. Bu elektrik alanının yardımıyla yüzey gerilim değerinin aşılması sayesinde Taylor konisi jet şekline dönmeye başlar ve daha sonra jet kararsız halde harekete başlar. Sabit dönme hızına sahip toplayıcı silindir üzerine liflerin toplanmaya başlaması ile nanolif yüzey oluşumu meydana gelir. Aynı zamanda liflerin toplayıcı silindir üzerine homojen olarak dağılabilmesi amacıyla silindir yatay eksende hareket etmeye başlar.

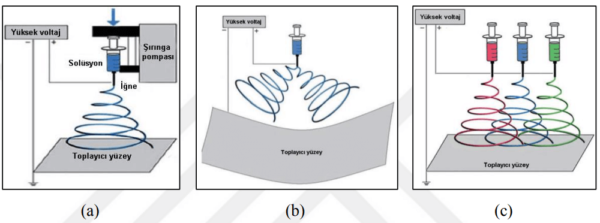
İğneli elektro lif çekim sistemleri;

• Tek iğneyle tek jet (Şekil 1.20 (a)),
• Tek iğne ile çoklu jet (Şekil 1.20 (b)),
• Çoklu iğne ile çoklu jet (Şekil 1.20 (c)),

oluşturanlar olmak üzere üç farklı yapıda kullanılabilmektedir.

Taylor Konisi Oluşumu

1960‘ larda Taylor konik bir geometride elektrik alan tarafından formu değişmiş bir damlacıktaki koşulları analiz etmiştir. Konik şekil, yük itme ve yüzey gerilim kuvvetlerinin birbiriyle ilişkisinden kaynaklanır. Şekil 1.21‘ de görüldüğü üzere iğne ucu ile bir karşı elektrot arasında elektrik alanı uygulandığında damlacık içinde hem normal hem de teğetsel bileşenler bir elektrik gerilimi ile yüklenir. Elektrostatik alanın gücü düşük olduğunda, iğne ucunda asılı duran damla, solüsyonun yüzey gerilimi nedeniyle damlamaz. Elektrik alanın yoğunluğu arttıkça, solüsyon yüzeyindeki yükler birbirini iter ve kayma gerilmeleri oluşturur. Bu itici kuvvetler yüzey gerilimine zıt yönde hareket eder, bu durum iğne ucundaki damlanın konik bir şekle ve daha sonra uzamasına neden olur.

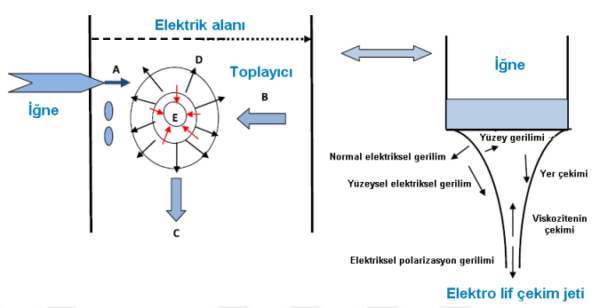
Şekil 1.21. Elektro lif çekimi sırasında yüklü damlacık üzerine etki eden kuvvetler; A: elektrostatik kuvvet, B: çekme kuvveti, C: yer çekimi, D: Coulomb itme kuvveti, E: yüzey gerilimi ve viskoelastik kuvvet.

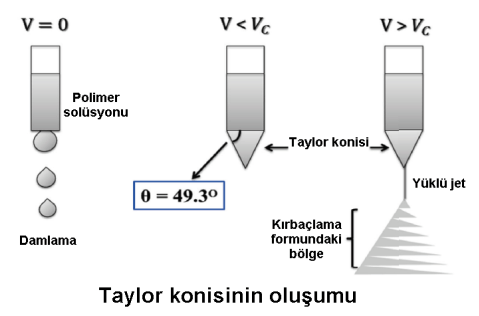
Taylor‘ a göre, bir elektrik alanındaki viskoz sıvı damlacıklarından ince filamentlerin oluşumu, elektrik kuvvetlerinin neden olduğu sıvı yüzeyinin maksimum kararsızlığından kaynaklanmaktadır. Ayrıca, Şekil 1.22‘ de gösterilen damlacık yarı dikey açılı bir koni biçimi aldığında, elektrik alanında 49,3 derece açıda viskoz bir sıvının dengede kaldığını göstermiştir.

Taylor konisi elektro lif çekim işleminde önemlidir çünkü lif oluşturma işleminde başlangıç eğilimlerini tanımlar. V > Vc olduğunda, ince bir solüsyon jeti koni yüzeyinden patlayacak ve zıt kutupların veya topraklamanın en yakın elektroduna doğru hareket edecektir. Bir diğer ifade ile, jet bir ucu başlangıç noktasına bağlı ve diğer ucu serbest bırakılan viskoelastik ortam ile bağlanan yüklü bir zincir yapısıdır. Yüzey gerilimi ile iğne ucunda tutulan polimer solüsyonu, bir elektrik alanına tabi tutulduğunda, sıvı yüzeyi elektrik yükü ile yüklenir. Karşılıklı yük itme hareketi sebebiyle, yüzey gerilim kuvvetlerine karşı diğer kuvvetler bir bütün olarak hareket eder ve akışkan solüsyonda kesme gerilmeleri oluşturur. Elektrik alanında artan yoğunluk ile solüsyonundaki aynı polariteye sahip iyonlar, damlanın üzerine birikmeye zorlanacaktır. Böylece kararlı jetin uzunluğu artan voltaj ile artacaktır.

Jet

İğne ucunda oluşan Taylor konisinden ileri doğru akmaya başlayan solüsyon jeti, eksen yönü boyunca birkaç milimetreden birkaç santimetreye kadar uzayabilen kısa bir bölüm için düzdür. Oluşan solüsyon jeti, elektrik yüklerini iğne ucundan dengelenmemiş iyonlar şeklinde taşır. Solüsyon jetindeki itme etkisine sebep olan yükler, denge koşulunu sağlamak için jet yüzeyine yarıçap doğrultusunda göç eder. Sonuç olarak elektrik alanı tarafından yüklenen elektrostatik kuvvet, jet yüzeyine uygulanır. Yüklü akışkan jetinin incelmesi ile birlikte elektrik alanının etkisi altında hızlanır.

Jet içindeki serbest yük ile harici elektrik alanı arasındaki etkileşimler, akışkan parametrelerine ve çalışma koşullarına bağlı olarak akış aşağı doğru sürüklenme ve yayılma hareketi yapan, farklı oranlarda büyüyen farklı kararsızlıklar arasında kuvvet değişkenliğine yol açar. Elektro lif çekiminin kontrol edilebilmesi, bu nedenle elektrik yüklü bir sıvı jetindeki kararsızlıklar arasındaki durumun anlaşılabileceği bir model geliştirilmiştir.

Kararsız Bölge

İlk kararlı aşamadan sonra jet tarafından taşınan yüklerin etkisi altında bükme, sarma, spiral ve döngü hareketlerini içerebilen kararsız bir aşamaya girer. Jet kararsızlığının varlığı, yüzey yüklerinin bozulmasının neden olduğu eksenel ve simetrik kararsızlıktan kaynaklanmaktadır. Eksenel simetrik kararsızlık, jet ekseninin bozulmasından kaynaklanır, bu da jetin farklı bölümlerinin farklı elektrostatik kuvvet altında olmasından dolayı düzensiz bir jet elde edilir.

Bu kararsızlıklar biriken liflerin büyüklüğünü ve geometrisini etkilemektedir. Rayleigh kararsızlığı olarak da bilinen ilk kararsızlık eksenel simetriktir ve elektrik alanının gücü düşük olduğunda veya solüsyonun viskozitesi optimum değerin altında olduğunda ortaya çıkar.  Çok düşük viskoziteli solüsyonların kullanılması, jet kopmalarına neden olur ve lif üzerinde boncuk morfolojisine yol açar. Bu durumun sebebi zayıf zincir dolaşma yoğunluğu ve elektrostatik alanın yetersiz olmasından kaynaklanmaktadır.

Rayleigh kararsızlığı, elektrik alan (yük) yoğunluğunun yükseltilmesi veya solüsyondaki polimer konsantrasyonunun yükseltilmesiyle ile azaltılabilir. Rayleigh kararsızlığı tarafından kontrol edilen jetin ilk düz yolunu takiben, polimer jeti bükülme ve whipping (kırbaçlanma) kararsızlıklarından da etkilenir. Bu kararsızlıklar, jetin içinde bulunan, jetin incelmesini ve uzamasını sağlayan aşırı yükler arasındaki yük-yük itilmesinden kaynaklanmaktadır. Yüksek elektrik kuvvetlerinde jet, eğilme ve whipping kararsızlığı tarafından baskındır ve jetin ters koni biçiminde hareket etmesine neden olur. Elektrik alanındaki voltaj arttıkça ve jet içindeki yük yoğunluğu yeterli olduğunda Rayleigh ve bükülme kararsızlıkları azalır ve eksenel ancak simetrik olmayan whipping kararsızlığı, jet üzerinde bükülme kuvveti üreterek, jetin yüksek derecede uzamasına neden olur. Elektro lif çekimi sırasında kararsızlık durumunun en önemli rolü jetin gerilmesidir. Solüsyon jetleri, çözücünün buharlaştırılması ile birlikte elektrostatik kuvvet altında toplayıcıya doğru uçar ve birikir.

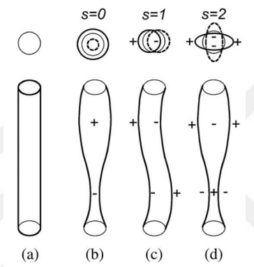
Şekil 1.23‘ de gösterilen üstten görünüşler, jetin en büyük salınım genliklerindeki enine kesitlerini ve jet uzunluğu boyunca farklı konumları temsil eden koyu ve kesik konturları göstermektedir. Yandan görünüşler ise jet boyunca şekil ve merkez çizgisindeki değişiklikleri gösterir. (+ / – ) ise jet şeklinden pozitif veya negatif sapma bölgelerini göstermek için kullanılır. Şekil 1.23‘ de;

• (a) Eğilmemiş silindirik akışkan elemanını,
• (b) İncelme (s = 0) kararsızlığını,
• (c) Whipping (kırbaçlama) (s = 1) kararsızlığını,
• (d) Bölünme (kopma) (s = 2) kararsızlığını,

ifade etmektedir. Kararsızlığın büyümesi, eşit boyutlu damlacıklara yol açar ve iki eşit büyüklükte alt jeti beraberinde getirir

---

T.C. ERCİYES ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
TEKSTİL MÜHENDİSLİĞİ ANABİLİM DALI

Hazırlayan Hüsnü AYDEMİR
Danışman Prof. Dr. Oğuz DEMİRYÜREK
Doktora Tezi Temmuz

2021 KAYSERİ
Kaynak linki